FUNCIÓN LINEAL
En geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es unalínea recta. Esta función se puede escribir como:
donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Si se modifica mentonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.
Algunos autores llaman función lineal a aquella con b= 0 de la forma:
mientras que llaman función afín a la que tiene la forma:
cuando b es distinto de cero.
EJEMPLO
Una función lineal de una única variable dependiente x es de la forma:
que se conoce como ecuación de la recta en el plano xy.
En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:
en esta recta el parámetro m= 1/2 por tanto de pendiente 1/2, es decir, cuando aumentamos x en una unidad entonces y aumenta en 1/2 unidad, el valor de b es 2, luego la recta corta el eje y en el punto y= 2.
En la ecuación:
la pendiente de la recta es el parámetro m= -1, es decir, cuando el valor de x aumenta en una unidad, el valor de ydisminuye en una unidad; el corte con el eje y es en y= 5, dado que el valor de b= 5.
En una recta el valor de m se corresponde al ángulo 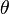 de inclinación de la recta con el eje de las x a través de la expresión:
de inclinación de la recta con el eje de las x a través de la expresión:
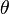 de inclinación de la recta con el eje de las x a través de la expresión:
de inclinación de la recta con el eje de las x a través de la expresión: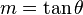
- PROBLEMAS DE
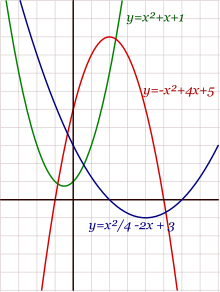
- En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida como:en donde a, b y c son números reales (constantes) y a es distinto de 0.La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso contrario. El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.La derivada de una función cuadrática es una función lineal y su integral una función cúbica.RAÍCESLas raíces (o ceros) de una función cuadrática, como en toda función, son los valores de x, para los cuales
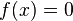 . Por tratarse de un polinomio de grado 2, habrá a lo sumo 2 raíces, denotadas habitualmente como:
. Por tratarse de un polinomio de grado 2, habrá a lo sumo 2 raíces, denotadas habitualmente como:  y
y 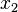 , dependiendo del valor del discriminante Δ definido como
, dependiendo del valor del discriminante Δ definido como  .
.- Dos soluciones reales y diferentes si el discriminante es positivo:
-
 .
.
- Una solución real doble si el discriminante es cero:
- Dos números complejos conjugados si el discriminante es negativo:
-

- Existen tres formas principales de escribir una función cuadrática, aplicables según el uso que se le quiera dar a la función: un estudio analítico de la función o de la ecuación cuadrática, una interpretación o construcción geométrica de la parábola, etc. Las tres formas son equivalentes.
- FORMA DESARROLLADA
- La forma desarrollada de una función cuadrática (o forma estándar) corresponde a la del polinomio de segundo grado, escrito convencionalmente como:con
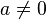 .
. -
- FORMA FACTORIZADA
- Toda función cuadrática se puede escribir en forma factorizada en función de sus raíces como:siendo a el coeficiente principal de la función, y
 y
y 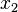 las raíces de
las raíces de  . En el caso de que el discriminante Δ sea igual a 0 entonces
. En el caso de que el discriminante Δ sea igual a 0 entonces  por lo que la factorización adquiere la forma:En este caso a
por lo que la factorización adquiere la forma:En este caso a se la denomina raíz doble, ya que su orden de multiplicidad es 2.FORMA CANONICA
se la denomina raíz doble, ya que su orden de multiplicidad es 2.FORMA CANONICA -
- Toda función cuadrática puede ser expresada mediante el cuadrado de un binomio de la siguiente manera:siendo a el coeficiente principal y el par ordenado (h;k) las coordenadas del vértice de la parábola.
Corte con el eje y
La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):lo que resulta:la función corta el eje y en el punto (0, c), siendo c el término independiente de la función.A este punto de la función también se lo conoce con Ordenada al OrigenCorte con el eje x
La función corta al eje x cuando y vale 0, dada la función:se tiene que:las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen, como es sabido, por la expresión: .
.
Si la función no corta al eje x, la fórmula anterior no tiene solución (en los reales).Extremos
Toda función cuadrática posee un máximo o un mínimo, que es el vértice de la parábola. Si la parábola tiene concavidad hacia arriba, el vértice corresponde a un mínimo de la función; mientras que si la parábola tiene concavidad hacia abajo, el vértice será un máximo.Dada la función en su forma desarrollada: , la coordenada x del vértice será simplemente:
, la coordenada x del vértice será simplemente:  . La coordenada y del vértice corresponde a la función f evaluada en ese punto.Dada la forma canónica:
. La coordenada y del vértice corresponde a la función f evaluada en ese punto.Dada la forma canónica: , las coordenadas explícitas del vértice son: (h,k).FUNCIÓN CUBICALa función cúbica es una función polinómica de tercer grado. Tiene la forma:
, las coordenadas explícitas del vértice son: (h,k).FUNCIÓN CUBICALa función cúbica es una función polinómica de tercer grado. Tiene la forma: ; donde el coeficiente a es distinto de 0.
; donde el coeficiente a es distinto de 0.
Tanto el dominio de definición como el conjunto imagen de estas funciones pertenecen a los números reales.La derivada de una función cúbica genera una función cuadrática y su integral una función cuádratica.ea un cuerpo conmutativo, donde se pueden extraer raíces, propiedad que hará posible resolver la ecuación.En un cuerpo algebraicamente cerrado se sabe que todo polinomio de tercer grado (o ecuación cúbica) tiene tres raíces. Este es el caso, por ejemplo, del cuerpo de los números complejos, según el Teorema Fundamental del Álgebra.La solución de la ecuación algebraica cúbica fue dada por primera vez en el libro Ars Magna (del latín, que significa Gran Arte o Arte Magno) por el matemático italianoGerolamo Cardano (1501-1576) que publicó en el año de 1545, razón por la cual se le llama método de Cardano.Los pasos de la resolución son:
un cuerpo conmutativo, donde se pueden extraer raíces, propiedad que hará posible resolver la ecuación.En un cuerpo algebraicamente cerrado se sabe que todo polinomio de tercer grado (o ecuación cúbica) tiene tres raíces. Este es el caso, por ejemplo, del cuerpo de los números complejos, según el Teorema Fundamental del Álgebra.La solución de la ecuación algebraica cúbica fue dada por primera vez en el libro Ars Magna (del latín, que significa Gran Arte o Arte Magno) por el matemático italianoGerolamo Cardano (1501-1576) que publicó en el año de 1545, razón por la cual se le llama método de Cardano.Los pasos de la resolución son:- Dividir la ecuación inicial por el coeficiente a (a ≠ 0). Se obtiene:
-
 con
con  ,
,  ,
,  .
.
- Proceder al cambio de incógnita
 , para suprimir el término cuadrado. En efecto, al desarrollar
, para suprimir el término cuadrado. En efecto, al desarrollar 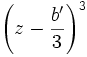 con la identidad precedente, vemos aparecer el término
con la identidad precedente, vemos aparecer el término  , compensado exactamente por
, compensado exactamente por 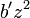 que aparece en
que aparece en  . Se obtiene:
. Se obtiene:
-
 , con p y q números del cuerpo que tienen las siguientes expresiones
, con p y q números del cuerpo que tienen las siguientes expresiones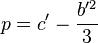
 .
.
- Y ahora, la astucia genial: escribir
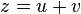 . Así, la ecuación precedente da
. Así, la ecuación precedente da  .
.
-
- Desarrollando:
 .
. - Reagrupando:
 .
. - Factorizando:
 .
.
- Desarrollando:
- Como se ha introducido una variable adicional (u y v en vez de z), es posible imponerse una condición adicional. Concretamente:
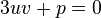 , que implica
, que implica 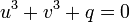 .
.
- Pongamos
 y
y  . Entonces tenemos
. Entonces tenemos  y
y  porque
porque  . Por lo tanto U y V son las raíces de la ecuación auxiliar
. Por lo tanto U y V son las raíces de la ecuación auxiliar  , que se sabe resolver.
, que se sabe resolver.
Luego y
y  son raíces cúbicas de
son raíces cúbicas de 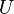 y
y  (que verifican
(que verifican  y finalmente
y finalmente  .En el cuerpo
.En el cuerpo , si
, si  y
y  son estas raíces cúbicas, entonces las otras son
son estas raíces cúbicas, entonces las otras son 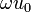 y
y 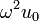 , y por supuesto
, y por supuesto  y
y  , con
, con 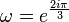 , una raíz cúbica de la unidad.Como el producto uv está fijado
, una raíz cúbica de la unidad.Como el producto uv está fijado , las parejas
, las parejas 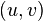 posibles son
posibles son 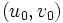 ,
,  y
y  .Las otras raíces de la ecuación de tercer grado son por lo tanto
.Las otras raíces de la ecuación de tercer grado son por lo tanto y
y  .DISCRIMINANTEResulta importante y a la vez esencial obtener propiedades elementales de los polinomios como herramientas de análisis en los resultados según los valores de sus coeficientes.
.DISCRIMINANTEResulta importante y a la vez esencial obtener propiedades elementales de los polinomios como herramientas de análisis en los resultados según los valores de sus coeficientes.- Demostración del discriminante
 mediante transformaciones de equivalencia de la ecuación auxiliar
mediante transformaciones de equivalencia de la ecuación auxiliar 
-
- Trinomio cuadrado perfecto

- Trinomio cuadrado perfecto
-
- Trasformación equivalente
 en
en 
- Trasformación equivalente
-
- Moviendo
 al miembro derecho
al miembro derecho 
- Moviendo
-
- Demostrado que

- EL CASO REAL
- cuando la ecuación posee raices Reales dobles.
- Demostrado que
Las primeras ecuaciones de tercer grado que se intentó resolver fueron con coeficientes reales (de hecho: enteros). El cuerpo de los reales no es algebraicamente cerrado, por lo tanto, el número de raíces reales no es siempre 3. Las que faltan se encuentran en C, extensión algebraica cerrada de R. La distinción aparece cuando se sacan las raíces cuadradas en el cálculo de U y V. Las raíces cúbicas no plantean problemas.Se demuestra que el número de raíces reales depende del discriminante de la ecuación auxiliar :
:- Si Δ < 0 existe una única raíz real. Las demás son complejas conjugadas.
- Si Δ = 0 existe una raíz múltiple real: una raíz triple o una doble y otra simple, todas reales.
- Si Δ > 0 existen tres raíces reales.
Habrán notado que siempre hay por lo menos una solución real. Es debido a que las funciones polinomiales no constantes tienen límites infinitos en +∞ y -∞ y las de grado impar tienen límites de signos contrarios. Como son funciones continuas, tienen que pasar por cero, por el teorema de los valores intermedios.En la figura siguiente se registra todos los casos, según los signos de a y de Δ.Aunque lo más fácil es resolverla con el método Newton-Raphson ya que sabemos que al menos habrá una solución real.La ecuación cúbica incompleta posee tres raíces reales cuando el discriminante
posee tres raíces reales cuando el discriminante 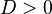 , pero donde
, pero donde  y
y 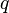 posee cualquier valor y signo. Tales raíces se calculan como
posee cualquier valor y signo. Tales raíces se calculan como , para
, para  donde el signo positivo se usa si
donde el signo positivo se usa si y el signo negativo se usa si
y el signo negativo se usa si  . Mientras que
. Mientras que  esta dada por
esta dada por De modo que si queremos calcular las tres raíces de la ecuación cúbica completa
De modo que si queremos calcular las tres raíces de la ecuación cúbica completa , entonces podemos obtenerlas fácilmente como
, entonces podemos obtenerlas fácilmente como , para
, para  RAICES MULTIPLESEn cualquier ecuación cúbica es posible que se presenten raíces múltiples, es decir, raíces de multiplicidad dos y tres, esto es, que dos o tres de las raíces sean iguales entre sí. Las raíces de multiplicidad unitaria ya fueron descritas antes, ahora la raíz doble se puede presentar si y sólo si se cumple la condición de que
RAICES MULTIPLESEn cualquier ecuación cúbica es posible que se presenten raíces múltiples, es decir, raíces de multiplicidad dos y tres, esto es, que dos o tres de las raíces sean iguales entre sí. Las raíces de multiplicidad unitaria ya fueron descritas antes, ahora la raíz doble se puede presentar si y sólo si se cumple la condición de que y las raíces de la ecuación cúbica incompleta serán
y las raíces de la ecuación cúbica incompleta serán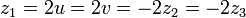 mientras que las raíces triples se presentan cuando se cumpla la condición de que
mientras que las raíces triples se presentan cuando se cumpla la condición de que con lo que las raíces de la ecuación cúbica completa se calcularán fácilmente como
con lo que las raíces de la ecuación cúbica completa se calcularán fácilmente como .EJEMPLOSea la ecuación cúbica
.EJEMPLOSea la ecuación cúbica , procedamos a resolverla. Para ello, sigamos los pasos descritos en el primer párrafo.
, procedamos a resolverla. Para ello, sigamos los pasos descritos en el primer párrafo. (al dividir por 2)
(al dividir por 2)- Con x = t + 1, es decir t = x - 1, reemplazando:
 , y desarrollando:
, y desarrollando: 
- x = u + v, U = u³, V = v³ y nos imponemos U + V = - 1 y UV = - 1. U y V son las raíces de X² + X - 1 = 0.
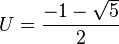 y
y  , luego
, luego ![u = \sqrt[3]{\frac {-1 - \sqrt {5}} {2}} \,](http://upload.wikimedia.org/math/0/2/8/028fb28ea5a3c116efa26ad70b76cfa7.png) y
y ![v = \sqrt[3]{\frac {-1 + \sqrt {5}} {2}} \,](http://upload.wikimedia.org/math/3/b/3/3b301c212acc6496fd958be984308ec0.png) .
.![t = x - 1 = u + v - 1 = \sqrt[3]{\frac {-1 - \sqrt {5}} {2}} + \sqrt[3]{\frac {-1 + \sqrt {5}} {2}} - 1 \approx -1,3221853546](http://upload.wikimedia.org/math/5/1/3/513472e74ff72db470860f9c127f9789.png)
FUNCIÓN EXPONENCIAL Y LOGARÍTMICASea un número real positivo. La función que a cada número real x le hace corresponder la potencia
un número real positivo. La función que a cada número real x le hace corresponder la potencia  se llama función exponencial de base a y exponente x. Como
se llama función exponencial de base a y exponente x. Como para todo
para todo 
 ,la función exponencial es una función de
,la función exponencial es una función de  en
en  . En el siguiente teorema, se presentan las propiedades más importantes de la función exponencial.
. En el siguiente teorema, se presentan las propiedades más importantes de la función exponencial.
Sean a y b reales positivos y x,yÎÂ ,entonces:1.
 2.
2. 3.
3. 4.
4. 5.
5. . 6 .
. 6 . Cuando a > 1 ,si x < y, entonces,
Cuando a > 1 ,si x < y, entonces, .Es decir, cuando la base a es mayor que 1,la función exponencial
.Es decir, cuando la base a es mayor que 1,la función exponencial
de base a es estrictamente creciente en su dominio.Cuando 0 < a < 1, si x < y , entonces, . Esto significa que la función exponencial de base a < 1 es estrictamente decreciente ensu dominio.
. Esto significa que la función exponencial de base a < 1 es estrictamente decreciente ensu dominio. . 10.Si 0< a < b ,se tiene:
. 10.Si 0< a < b ,se tiene:
 . Esta propiedad permite comparar funciones exponenciales de diferentes bases.11. Cualquiera que sea el número real positivo
. Esta propiedad permite comparar funciones exponenciales de diferentes bases.11. Cualquiera que sea el número real positivo
 ,existe un único número real
,existe un único número real tal que
tal que  . Esta propiedad indica que la función exponencial es sobreyectiva. Cuando x e y son enteros, los propiedades enunciadas anteriormente pueden demostrarse usando las definiciones y el teorema 1. Para el caso en el cual x e y son racionales, la demostración utiliza la definición y el teorema 2. Para el caso general, es decir, cuando x e yson reales, la demostración utiliza elementos del análisis real.
. Esta propiedad indica que la función exponencial es sobreyectiva. Cuando x e y son enteros, los propiedades enunciadas anteriormente pueden demostrarse usando las definiciones y el teorema 1. Para el caso en el cual x e y son racionales, la demostración utiliza la definición y el teorema 2. Para el caso general, es decir, cuando x e yson reales, la demostración utiliza elementos del análisis real.
Gráfica de la Función Exponencial
En relación con las propiedades 7 y 8, enunciadas en el teorema, es conveniente hacer algunos comentarios adicionales.En primer lugar, en las figuras 1 y 2, aparecen las gráficas de algunas funciones exponenciales de base a > 1 (fig. 1) y de base a < 1 (fig. 2).
 Note que cuando la base a es mayor que 1,la función exponencial
Note que cuando la base a es mayor que 1,la función exponencial (fig.1) no está acotada superiormente. Es decir ,
(fig.1) no está acotada superiormente. Es decir ,  crece sin límite al aumentar la variable x. Además, ésta función tiene al cero como extremo inferior. Esto es ,
crece sin límite al aumentar la variable x. Además, ésta función tiene al cero como extremo inferior. Esto es ,  tiende a cero(0), cuando x toma valores grandes pero negativos. Igualmente, cuando la base a < 1, la función exponencial
tiende a cero(0), cuando x toma valores grandes pero negativos. Igualmente, cuando la base a < 1, la función exponencial (fig.2) no está acotada superiormente, pero su comportamiento para valores grandes de x, en valor absoluto, es diferente. Así,
(fig.2) no está acotada superiormente, pero su comportamiento para valores grandes de x, en valor absoluto, es diferente. Así,  crece sin límite, al tomar x valores grandes, pero negativos y
crece sin límite, al tomar x valores grandes, pero negativos y  tiende a cero, cuando la variable x toma valores grandes positivos. El hecho de ser la función exponencial
tiende a cero, cuando la variable x toma valores grandes positivos. El hecho de ser la función exponencial con a > 1, estrictamente creciente (estrictamente decreciente cuando 0 < a < 1), significa que la función exponencial es inyectiva en su dominio.Este hecho y la continuidad de la función son las condiciones que se exigen para garantizar la existencia de la función inversa ( función logarítmica), que se presentan en la próxima sección. En relación con la propiedad 9, en un sentido, se deduce fácilmente de la definición de función; y, en otro, del hecho de ser la función exponencial inyectiva.Observación.Cuando a = e ,donde e es el número irracional cuya representación decimal con sus primeras cifras decimales, es e = 2.7182818284….,la función exponencial
con a > 1, estrictamente creciente (estrictamente decreciente cuando 0 < a < 1), significa que la función exponencial es inyectiva en su dominio.Este hecho y la continuidad de la función son las condiciones que se exigen para garantizar la existencia de la función inversa ( función logarítmica), que se presentan en la próxima sección. En relación con la propiedad 9, en un sentido, se deduce fácilmente de la definición de función; y, en otro, del hecho de ser la función exponencial inyectiva.Observación.Cuando a = e ,donde e es el número irracional cuya representación decimal con sus primeras cifras decimales, es e = 2.7182818284….,la función exponencial ,se llama: función exponencial de base e y, frecuentemente, se denota por Exp( x ) =
,se llama: función exponencial de base e y, frecuentemente, se denota por Exp( x ) =  .
.
2.1.3 Las Funciones Hiperbólicas
En algunos problemas de Física e Ingeniería, se presentan ciertas combinaciones de las funciones y
y  que por su interés y características especiales merecen ser consideradas con algún tratamiento. Tales combinaciones reciben el nombre de funciones hiperbólicas. Aquí solamente, se definirán y presentarán algunas identidades básicas que las relacionan.La función COSENO HIPERBÓLICO, denotada por coshx, se define:
que por su interés y características especiales merecen ser consideradas con algún tratamiento. Tales combinaciones reciben el nombre de funciones hiperbólicas. Aquí solamente, se definirán y presentarán algunas identidades básicas que las relacionan.La función COSENO HIPERBÓLICO, denotada por coshx, se define: ,
,  La función SENO HIPERBÓLICO, denotada por senhx , se define:
La función SENO HIPERBÓLICO, denotada por senhx , se define: ,
,  A partir de éstas, se definen las funciones: TANGENTE, COTANGENTE, SECANTE Y COSECANTE HIPERBÓLICA, de la siguiente manera:
A partir de éstas, se definen las funciones: TANGENTE, COTANGENTE, SECANTE Y COSECANTE HIPERBÓLICA, de la siguiente manera:


 A partir de la definición de las funciones hiperbólicas, es fácil demostrar, y se deja como ejercicio para el lector, las siguientes identidades con funciones hiperbólicas:1.
A partir de la definición de las funciones hiperbólicas, es fácil demostrar, y se deja como ejercicio para el lector, las siguientes identidades con funciones hiperbólicas:1. 2.
2. 3.
3. 4.
4. 5.
5. 6. senh2x =2senhx coshx8.
6. senh2x =2senhx coshx8. 9.
9. 10.
10. 11.
11. 12.
12. FUNCIÓN RACIONAL
FUNCIÓN RACIONAL
La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.
Las funciones racionales son del tipo: El dominio de una función racional de lo forman todos los números reales menos los valores de x que anulan el denominador.Ejemplo
El dominio de una función racional de lo forman todos los números reales menos los valores de x que anulan el denominador.Ejemplo
Construcción de hipérbolas
1. Traslación vertical
2. Traslación horizontal
3. Traslación oblicua

 Un tipo de función racional es la función de proporcionalidad inversa de ecuación:
Un tipo de función racional es la función de proporcionalidad inversa de ecuación: .
. Sus gráficas son hipérbolas. También son hipérbolas las gráficas de las funciones
Sus gráficas son hipérbolas. También son hipérbolas las gráficas de las funciones
 Las hipérbolas
Las hipérbolas son las más sencillas de representar.Sus asítontas son los ejesEl centro de la hipérbola, que es el punto donde se cortan las asíntotas, es el origen.
son las más sencillas de representar.Sus asítontas son los ejesEl centro de la hipérbola, que es el punto donde se cortan las asíntotas, es el origen.
 A partir de estas hipérbolas se obtienen otras por traslación.
A partir de estas hipérbolas se obtienen otras por traslación. El centro de la hipérbola es: (0, a).Si a>0,
El centro de la hipérbola es: (0, a).Si a>0, se desplaza hacia arriba a unidades.
se desplaza hacia arriba a unidades.
 El centro de la hipérbola es: (0, 3)Si a<0,
El centro de la hipérbola es: (0, 3)Si a<0, se desplaza hacia abajo a unidades.
se desplaza hacia abajo a unidades.
 El centro de la hipérbola es: (0, -3)
El centro de la hipérbola es: (0, -3) El centro de la hipérbola es: (-b, 0).Si b> 0,
El centro de la hipérbola es: (-b, 0).Si b> 0, se desplaza a la izquierda b unidades.
se desplaza a la izquierda b unidades.
 El centro de la hipérbola es: (-3, 0)Si b<0,
El centro de la hipérbola es: (-3, 0)Si b<0, se desplaza a la derecha b unidades.
se desplaza a la derecha b unidades.
 El centro de la hipérbola es: (3, 0)
El centro de la hipérbola es: (3, 0) El centro de la hipérbola es: (-b, a)
El centro de la hipérbola es: (-b, a)
 El centro de la hipérbola es: (3, 4).Para representar hipérbolas del tipo:
El centro de la hipérbola es: (3, 4).Para representar hipérbolas del tipo: se divide y se escribe como:
se divide y se escribe como: Su representación gráfica es una hipérbola de centro (-b, a) y de asíntotas paralelas a los ejes.
Su representación gráfica es una hipérbola de centro (-b, a) y de asíntotas paralelas a los ejes.



REPRESENTACIÓN ANALÍTICA
APLICACIÓN
FUNCIÓN CUADRÁTICA






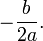





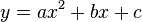


No hay comentarios:
Publicar un comentario